TR2019-154
QNTRPO: Including Curvature in TRPO
-
- , "QNTRPO: Including Curvature in TRPO", Optimization Foundations for Reinforcement Learning Workshop at NeurIPS, December 2019.BibTeX TR2019-154 PDF Software
- @inproceedings{Jha2019dec,
- author = {Jha, Devesh K. and Raghunathan, Arvind and Romeres, Diego},
- title = {{QNTRPO: Including Curvature in TRPO}},
- booktitle = {Optimization Foundations for Reinforcement Learning Workshop at NeurIPS},
- year = 2019,
- month = dec,
- url = {https://www.merl.com/publications/TR2019-154}
- }
- , "QNTRPO: Including Curvature in TRPO", Optimization Foundations for Reinforcement Learning Workshop at NeurIPS, December 2019.
-
MERL Contacts:
-
Research Areas:
Artificial Intelligence, Machine Learning, Optimization, Robotics
Abstract:
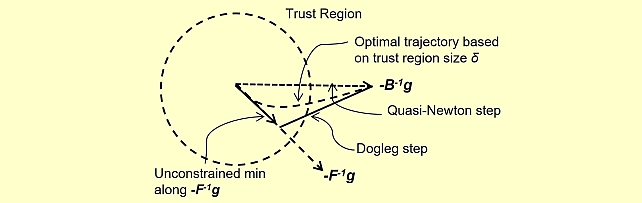
We propose a trust region method for policy optimization that employs QuasiNewton approximation for the Hessian, called Quasi-Newton Trust Region Policy Optimization (QNTRPO). Gradient descent is the de facto algorithm for reinforcement learning tasks with continuous controls. The algorithm has achieved state-of-the-art performance when used in reinforcement learning across a wide range of tasks. However, the algorithm suffers from a number of drawbacks including: lack of stepsize selection criterion, and slow convergence. We investigate the use of a trust region method using dogleg step and a Quasi-Newton approximation for the Hessian for policy optimization. We demonstrate through numerical experiments over a wide range of challenging continuous control tasks that our particular choice is efficient in terms of number of samples and improves performance
Software & Data Downloads
Related Publications
- @inproceedings{Jha2019oct,
- author = {Jha, Devesh K. and Raghunathan, Arvind and Romeres, Diego},
- title = {{Quasi-Newton Trust Region Policy Optimization}},
- booktitle = {Conference on Robot Learning (CoRL)},
- year = 2019,
- editor = {Leslie Pack Kaelbling and Danica Kragic and Komei Sugiura},
- pages = {945--954},
- month = oct,
- publisher = {Proceedings of Machine Learning Research},
- url = {https://www.merl.com/publications/TR2019-120}
- }