TR2014-019

Application of numerical optimization to the design of InP-based wavelength combiners

    •  Ozbayat, S., Kojima, K., Koike-Akino, T., Wang, B., Parsons, K., Singh, S., Nishikawa, S., Yagyu, E., "Application of Numerical Optimization to the Design of InP-based Wavelength Combiners", Optics Communications, DOI: 10.1016/​j.optcom.2014.02.030, Vol. 322, pp. 131-136, July 2014.
      BibTeX TR2014-019 PDF
      • @article{Ozbayat2014jul,
      • author = {Ozbayat, S. and Kojima, K. and Koike-Akino, T. and Wang, B. and Parsons, K. and Singh, S. and Nishikawa, S. and Yagyu, E.},
      • title = {Application of Numerical Optimization to the Design of InP-based Wavelength Combiners},
      • journal = {Optics Communications},
      • year = 2014,
      • volume = 322,
      • pages = {131--136},
      • month = jul,
      • publisher = {Optics Communications},
      • doi = {10.1016/j.optcom.2014.02.030},
      • issn = {0030-4018},
      • url = {https://www.merl.com/publications/TR2014-019}
      • }
  • MERL Contacts:
  • Research Area:

    Electronic and Photonic Devices

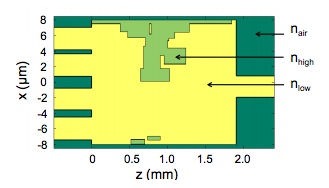
TR Image
Effective refractive indes distribution of the optimized 4x1 wavelength combiner with 16 patches.
Abstract:

We applied a numerical device optimization scheme, where tens of parameters can be optimized simultaneously with multiple target performance criteria that are given. The key items of the design scheme are the selection of the best optimization algorithm, metric, and consideration for fabrication errors. This method was then applied to design an MMI beam combiner with rectangular effective refractive steps with up to 75 parameters, and we obtained a simulated insertion loss of 0.8 dB for a 1.4 mm-long 2x1 wavelength combiner, and a simulated insertion loss of 4.2 dB for a 1.9 mm-long 4x1 wavelength combiner, both with 20 nm wavelength spacing. This methodology could also be applied to other types of optical devices.