TR2013-008
Nonlinear Camera Response Functions and Image Deblurring: Theoretical Analysis and Practice
-
- , "Nonlinear Camera Response Functions and Image Deblurring: Theoretical Analysis and Practice", IEEE Transactions on Pattern Analysis and Machine Intelligence, DOI: 10.1109/TPAMI.2013.40, Vol. 35, No. 10, February 2013.BibTeX TR2013-008 PDF
- @article{Tai2013feb,
- author = {Tai, Y.-W. and Chen, X. and Kim, S. and Kim, S.J. and Li, F. and Yang, J. and Yu, J. and Matsushita, Y. and Brown, M.S.},
- title = {Nonlinear Camera Response Functions and Image Deblurring: Theoretical Analysis and Practice},
- journal = {IEEE Transactions on Pattern Analysis and Machine Intelligence},
- year = 2013,
- volume = 35,
- number = 10,
- month = feb,
- doi = {10.1109/TPAMI.2013.40},
- issn = {0162-8828},
- url = {https://www.merl.com/publications/TR2013-008}
- }
- , "Nonlinear Camera Response Functions and Image Deblurring: Theoretical Analysis and Practice", IEEE Transactions on Pattern Analysis and Machine Intelligence, DOI: 10.1109/TPAMI.2013.40, Vol. 35, No. 10, February 2013.
-
Research Area:
Abstract:
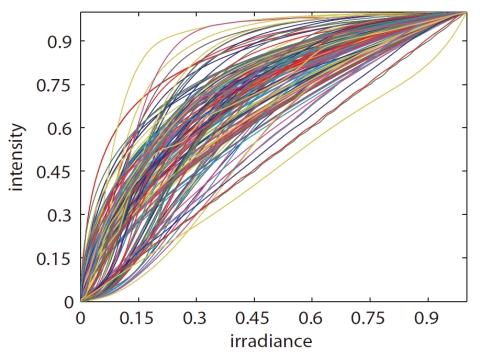
This paper investigates the role that nonlinear camera response functions (CRFs) have on image deblurring. We present a comprehensive study to analyze the effects of CRFs on motion deblurring. In particular, we show how nonlinear CRFs can cause a spatially invariant blur to behave as a spatially varying blur. We prove that such nonlinearity can cause large errors around edges when directly applying deconvolution to a motion blurred image without CRF correction. These errors are inevitable even with a known point spread function (PSF) and with state-of-the-art regularization based deconvolution algorithms. In addition, we show how CRFs can adversely affect PSF estimation algorithms in the case of blind deconvolution. To help counter these effects, we introduce two methods to estimate the CRF directly from one or more blurred images when the PSF is known or unknown. Our experimental results on synthetic and real images validate our analysis and demonstrate the robustness and accuracy of our approaches.
Related News & Events
-
NEWS IEEE Transactions on Pattern Analysis and Machine Intelligence: publication by MERL researchers and others Date: February 14, 2013
Where: IEEE Transactions on Pattern Analysis and Machine Intelligence
Research Area: Computer VisionBrief- The article "Nonlinear Camera Response Functions and Image Deblurring: Theoretical Analysis and Practice" by Tai, Y-W, Chen, X., Kim, S., Kim, S.J., Li, F., Yang, J., Yu, J., Matsushita, Y. and Brown, M.S. was published in IEEE Transactions on Pattern Analysis and Machine Intelligence.