TR2013-007
Hybrid Control Lyapunov Functions for the Stabilization of Hybrid Systems
-
- , "Hybrid Control Lyapunov Functions for the Stabilization of Hybrid Systems", Hybrid Systems: Computation and Control (HSCC), DOI: 10.1145/2461326.2461341, April 2013, pp. 73-82.BibTeX TR2013-007 PDF
- @inproceedings{DiCairano2013apr,
- author = {{Di Cairano}, S. and Heemeis, W.P.M.H. and Lazar, M. and Bemporad, A.},
- title = {{Hybrid Control Lyapunov Functions for the Stabilization of Hybrid Systems}},
- booktitle = {Hybrid Systems: Computation and Control (HSCC)},
- year = 2013,
- pages = {73--82},
- month = apr,
- doi = {10.1145/2461326.2461341},
- isbn = {978-1-4503-1567-8},
- url = {https://www.merl.com/publications/TR2013-007}
- }
- , "Hybrid Control Lyapunov Functions for the Stabilization of Hybrid Systems", Hybrid Systems: Computation and Control (HSCC), DOI: 10.1145/2461326.2461341, April 2013, pp. 73-82.
-
MERL Contact:
-
Research Area:
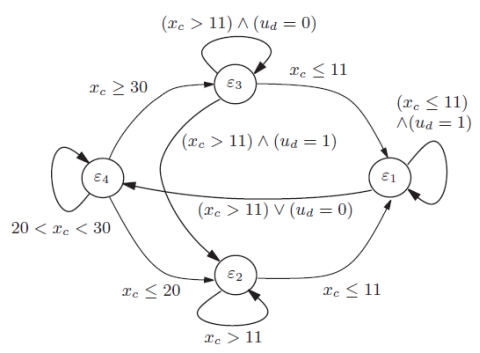
Abstract:
The design of stabilizing controllers for hybrid systems is particularly challenging due to the heterogeneity present within the system itself. In this paper we propose a constructive procedure to design stabilizing dynamic controllers for a fairly general class of hybrid systems. The proposed technique is based on the concept of a hybrid control Lyapunov function (hybrid CLF) that was previously introduced by the authors. In this paper we generalize the concept of hybrid control Lyapunov function, and we show that the existence of a hybrid CLF guarantees the existence of a standard control Lyapunov function (CLF) for the hybrid system. We provide a constructive procedure to design a hybrid CLF and the corresponding dynamic control law, which is stabilizing because of the established connection to a standard CLF that becomes a Lyapunov function for the closed-loop system. The obtained control law can be conveniently implemented by constrained predictive control in the form of a receding horizon control strategy. A numerical example highlighting the features of the proposed approach is presented.
Related News & Events
-
NEWS Hybrid Systems: Computation and Control (HSCC) 2013: publication by Stefano Di Cairano and others Date: April 8, 2013
Where: Hybrid Systems: Computation and Control (HSCC)
MERL Contact: Stefano Di Cairano
Research Area: Control
