TR2012-098
Topological Chaos, Braiding and Bifurcation of Almost-cyclic Sets
-
- , "Topological Chaos, Braiding and Bifurcation of Almost-cyclic Sets", AIP Chaos, Vol. 22, No. 4, December 2012.BibTeX TR2012-098 PDF
- @article{Grover2012dec,
- author = {Grover, P. and Ross, S. and Stremler, M. and Kumar, P.},
- title = {{Topological Chaos, Braiding and Bifurcation of Almost-cyclic Sets}},
- journal = {AIP Chaos},
- year = 2012,
- volume = 22,
- number = 4,
- month = dec,
- url = {https://www.merl.com/publications/TR2012-098}
- }
- , "Topological Chaos, Braiding and Bifurcation of Almost-cyclic Sets", AIP Chaos, Vol. 22, No. 4, December 2012.
-
Research Area:
Abstract:
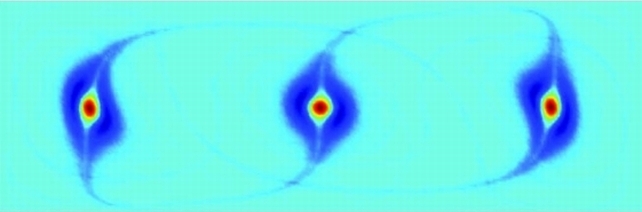
In certain two-dimensional time-dependent flows, the braiding of periodic orbits provides a way to analyze chaos in the system through application of the Thurston-Nielsen classification theorem (TNCT). We expand upon earlier work that introduced the application of the TNCT to braiding of almost-cyclic sets, which are individual components of almost-invariant sets [Stremler et al., "Topological chaos and periodic braiding of almost-cyclic sets", Phys. Rev. Lett. 106, 114101 (2011)]. In this context, almost-cyclic sets are periodic regions in the flow with high local residence time that act as stirrers or "ghost rods" around which the surrounding fluid appears to be stretched and folded. In the present work, we discuss the bifurcation of the almost-cyclic sets as a system parameter is varied, which results in a sequence of topologically distinct braids. We show that, for Stokes' flow in a lid-driven cavity, these various braids give good lower bounds on the topological entropy over the respective parameter regimes in which they exist. We make the case that a topological analysis based on spatiotemporal braiding of almost-cyclic sets can be used for analyzing chaos in fluid flows. Hence, we further develop a connection between set-oriented statistical methods and topological methods, which promises to be an important analysis tool in the study of complex systems.
Related News & Events
-
NEWS AIP Chaos: publication by Piyush Grover and others Date: December 1, 2012
Where: AIP Chaos
Research Area: Dynamical SystemsBrief- The article "Topological Chaos, Braiding and Bifurcation of Almost-cyclic Sets" by Grover, P., Ross, S., Stremler, M. and Kumar, P. was published in AIP Chaos.