TR2011-056
A Parallel Quadratic Programming Algorithm for Model Predictive Control
-
- , "A Parallel Quadratic Programming Algorithm for Model Predictive Control", World Congress of the International Federation of Automatic Control (IFAC), August 2011, vol. 18.BibTeX TR2011-056 PDF Software
- @inproceedings{Brand2011aug,
- author = {Brand, M. and Shilpiekandula, V. and Bortoff, S.A.},
- title = {A Parallel Quadratic Programming Algorithm for Model Predictive Control},
- booktitle = {World Congress of the International Federation of Automatic Control (IFAC)},
- year = 2011,
- volume = 18,
- month = aug,
- url = {https://www.merl.com/publications/TR2011-056}
- }
- , "A Parallel Quadratic Programming Algorithm for Model Predictive Control", World Congress of the International Federation of Automatic Control (IFAC), August 2011, vol. 18.
-
MERL Contacts:
-
Research Areas:
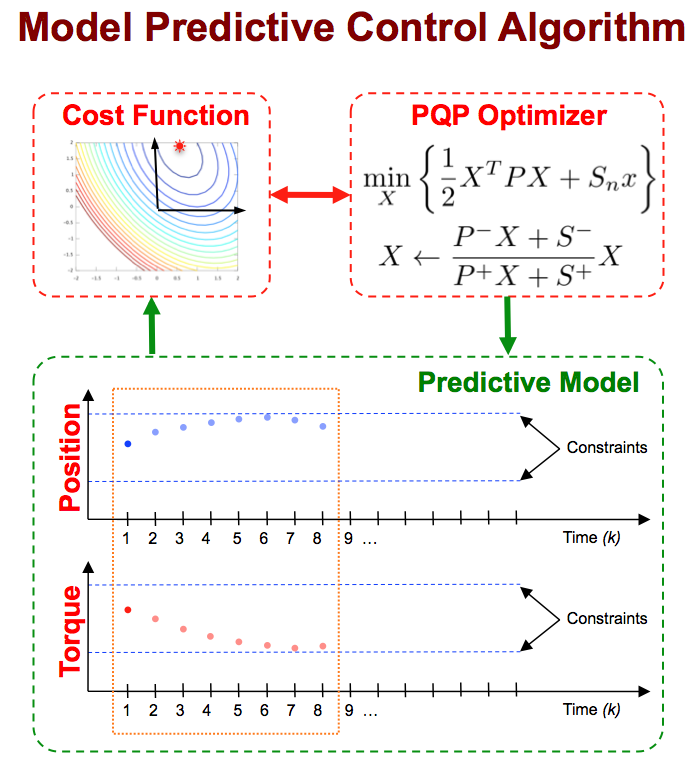
Abstract:
In this paper, an iterative multiplicative algorithm is proposed for the fast solution of quadratic programming (QP) problems that arise in the real-time implementation of Model Predictive Control (MPC). The proposed algorithm--Parallel Quadratic Programming (PQP)--is amenable to fine-grained parallelization. Conditions on the convergence of the PQP algorithm are given and proved. Due to its extreme simplicity, even serial implementations offer considerable speed advantages. To demonstrate, PQP is applied to several simulation examples, including a stand-alone QP problem and two MPC examples. When implemented in MATLAB using single-thread computations, numerical simulations of PQP demonstrate a 5 - 10x speed-up compared to the MATLAB active-set based QP solver quadprog. A parallel implementation would offer a further speed-up, linear in the number of parallel processors.
Software & Data Downloads
Related News & Events
-
NEWS MERL's High-speed optimization algorithms showcased at Mitsubishi Electric Corporation annual R&D Open House Date: February 13, 2014
MERL Contact: Matthew BrandBrief- Mitsubishi Electric Corporation announced its development of advanced optimization algorithms and high-speed calculation methods aimed at optimizing the performance of three practical systems: laser-processing machines for high-speed cutting of sheet metal using the shortest possible trajectories, moon probes achieved with minimized fuel consumption, and particle beam therapies for prompt medical treatments.
-
NEWS IFAC 2011: 2 publications by Matthew E. Brand, Scott A. Bortoff and Vijay Shilpiekandula Date: August 28, 2011
Where: World Congress of the International Federation of Automatic Control (IFAC)
MERL Contacts: Scott A. Bortoff; Matthew BrandBrief- The papers "Integrated Design and Control of Flexure-Based Nanopositioning Systems - Part I: Methodology" by Shilpiekandula, V. and Youcel-Toumi, K. and "A Parallel Quadratic Programming Algorithm for Model Predictive Control" by Brand, M., Shilpiekandula, V. and Bortoff, S.A. were presented at the World Congress of the International Federation of Automatic Control (IFAC).