TR2009-015
Distributed Opportunistic Scheduling With Two-Level Channel Probing
-
- , "Distributed Opportunistic Scheduling with Two-Level Channel Probing", IEEE Conference on Computer Communications (INFOCOM), April 2009.BibTeX TR2009-015 PDF
- @inproceedings{Thejaswi2009apr,
- author = {Thejaswi, C. and Pun, M.-O. and Zhang, J. and Poor, H.V.},
- title = {{Distributed Opportunistic Scheduling with Two-Level Channel Probing}},
- booktitle = {IEEE Conference on Computer Communications (INFOCOM)},
- year = 2009,
- month = apr,
- url = {https://www.merl.com/publications/TR2009-015}
- }
- , "Distributed Opportunistic Scheduling with Two-Level Channel Probing", IEEE Conference on Computer Communications (INFOCOM), April 2009.
-
MERL Contact:
-
Research Area:
Abstract:
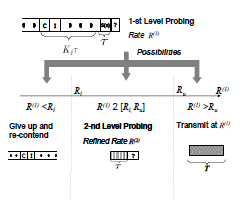
Distributed opportunistic scheduling (DOS) is studied for wireless ad-hoc networks in which many links contend for the channel using random access before data transmissions. Simply put, DOS involves a process of joint channel probing and distributed scheduling for ad-hoc (peer-to-peer) communications. Since in practice, link conditions are estimated with noisy observations, the transmission rate has to be backed off from the estimated rate to avoid transmission outages. Then, a natural question to ask is whether it is worthwhile for the link with successful contention to perform further channel probing to mitigate estimation errors, at the cost of additional probing. Thus motivated, this work investigates DOS with two-level channel probing by optimizing the tradeoff between the throughput gain from more accurate rate estimation and the resulting additional delay. Capitalizing on optimal stopping theory with incomplete information, it is shown that the optimal scheduling policy is threshold-based and is characterized by either one or two thresholds, depending on network settings. The necessary and sufficient conditions for both cases are rigorously established. In particular, our analysis reveals that performing second-level channel probing is optimal when the first-level estimated channel condition falls in between the two thresholds. Finally, numerical results are provided to illustrate the effectiveness of the proposed DOS with two-level channel probing.
Related News & Events
-
NEWS INFOCOM 2009: publication by Jinyun Zhang and others Date: April 19, 2009
Where: IEEE Conference on Computer Communications (INFOCOM)
MERL Contact: Jinyun Zhang
Research Area: CommunicationsBrief- The paper "Distributed Opportunistic Scheduling with Two-Level Channel Probing" by Thejaswi, C., Pun, M.-O., Zhang, J. and Poor, H.V. was presented at the IEEE Conference on Computer Communications (INFOCOM).
-
AWARD INFOCOM 2009 Best Paper Award Date: April 1, 2009
Awarded to: Chandrashekhar Thejaswi P.S., Junshan Zhang and Vincent Poor
Awarded for: "Distributed Opportunistic Scheduling with Two-Level Channel Probing"
Awarded by: IEEE Conference on Computer Communications (INFOCOM)
Research Area: Communications
