Optimal Route Planning under Uncertainty
| Citation: | Nikolova, E.; Brand, M.; Karger, D.R., "Optimal Route Planning under Uncertainty", International Conference on Automated Planning and Scheduling (ICAPS), June 2006 (ICAPS 2006) |
| MERL Report: | TR2006-060 |
Minimum-cost envelopes for the same network under quadratic and quadratic+exponential cost functions superimposed in a neighborhood of their global optima.
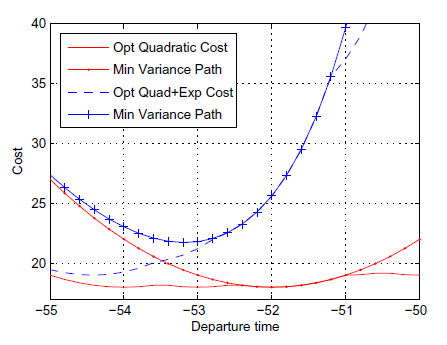
We present new complexity results and efficient algorithms for optimal route planning in the presence of uncertainty. We employ a decision theoretic framework for defining the optimal route: for a given source S and destination T in the graph, we seek an ST-path of lowest expected cost where the edge travel trimes are eandom variable and the cost is a nonlinear function of total travel time. Although this is a natural model for route-planning on real-world road networks, results are sparse due to the analytic difficulty of finding closed form expressions for the exptected cost (Fan, Kalaba and Moore), as well as the computational/combinatorial difficulty of efficiently finding an optimal path which minimizes the exptected cost. We identify a family of appropriate cost models and travel time distributions that are closed under convolution and physically valid. We obtain hardness results for routing problems with a given start time and cost functions with a global minimum, in a variety of deterministic and stochastic settings. In general the global cost is not separable into edge costs, precluding classic shortest-path approaches. However, using partial minimization techniques, we exhibit an efficient solution via dynamic programming with low polynomial complexity.
 | Read the full technical report (PDF: 172.2 kB) |