Fast Low-Rank Modifications of the Think Singular Value Decomposition
Citation: Brand, M., "Fast Low-Rank Modifications of the Thin Singular Value Decomposition", Linear Algebra and Its Applications, Vol. 415, Issue 1, pp. 20-30, May 2006 (Elsevier Science Direct)
Run-time of sequential SVD updating (solid line) versus batch Lanczos (dashed line), as a function of the number of singular vector/value triplets computed from a random matrix.
Date:
May 2006
MERL Contact: Matthew Brand
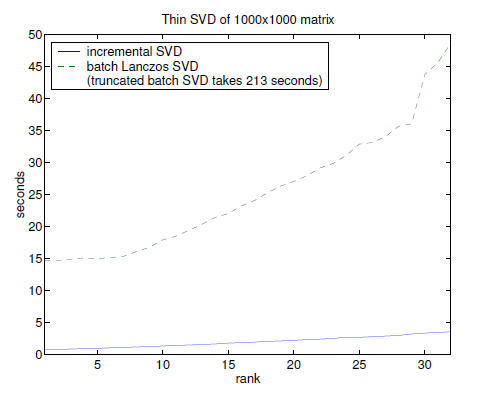
Abstract: This paper develops an identity for additive modivations of a singular value decomposition (SVD) to reflect updates, downdates, shifts, and edits of the data matrix. This sets the stage for fast and ememory-efficient sequential algorithms for tracking singular values and subspaces. In conjunction with a fast solution for the pseudo-inverse of a submatrix of an orthogonal matrix, we develop a scheme for computing a thin SVD of streaming data in a single pass with linear time complexity: A rank-r think SVD of a p x q matrix can be computed in O(pqr) time for r <= √min(p,q).
 | Read the full technical report (PDF: 228.2 kB) |